Phylogenetic Treatment of Recombination

With a particular focus on Bacterial Recombination

Tim Vaughan

cEvo group, D-BSSE, The ETH Zurich

Taming the BEAST, 22^nd Feb, 2019

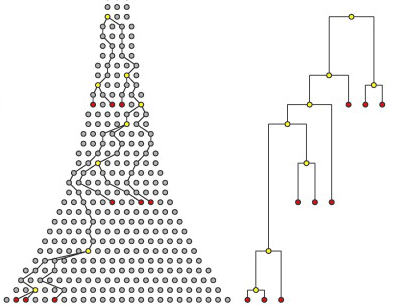
Recombination primer

Occurs in eukaryotes, bacteria and viruses.
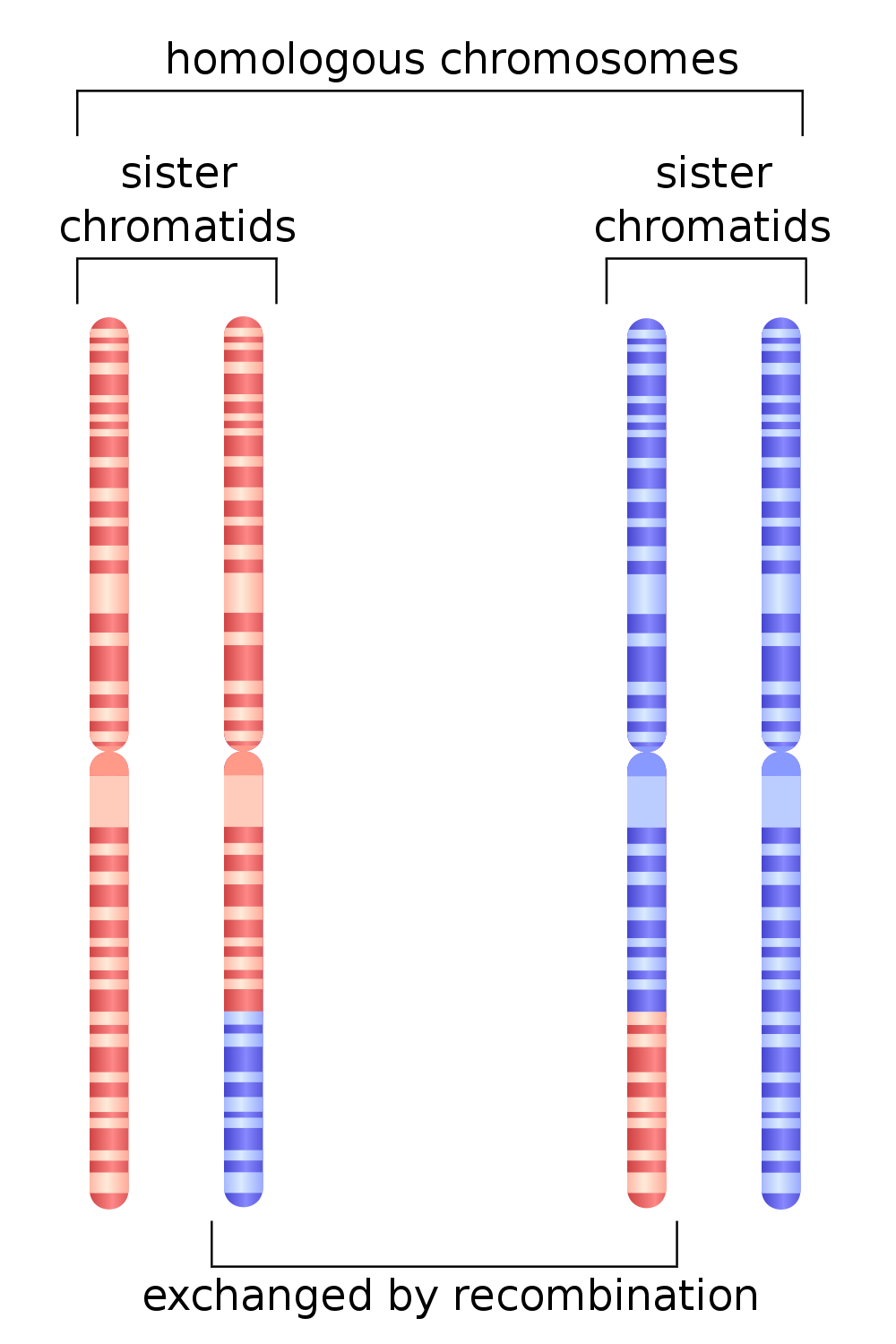
Eukaryotic recombination occurs during meiosis via chromosomal crossover.
Bacterial recombination occurs via
- phage-mediated transduction,
- natural transformation, and
- conjugation.
Viral recombination occurs when multiple strains infect a single cell. (Example: reassortment in segmented viral genomes.)

commons.wikimedia.org

Recombination and Phylogenetics

Ignoring recombination when present:

Biases inference of internal node heights times.
Biases inference of topology.
Poor mixing due to badly fitting model.

Relationship to Species Phylogenies

Recombination affects gene phylogenies.
Species phylogeny may also be a network! (See Zhang et al., MBE, 2017.)

Accounting for Recombination

Pre-process of data to identify and remove non-vertically inherited material.

Pros	Cons
Can use standard tools for phylogenetic inference.	Data is being thrown away. Ad hoc, may bias results.

Explicitly model recombination processes.

Pros	Cons
Can make use of all data. Can infer additional parameters such as recombination rates. May yield increased confidence in estimates.	Models can be complex, with many parameters. Both computationally and statistically challenging.

Wright-Fisher with Recombination

Consider an WF model with male and female diploid individuals.
Focus on a small segment of the genome.

Each child selects 1 male and 1 female parent uniformly at random.
With probability $r$ (which depends on the segment size) the two chromosome pairs of a parent are recombined before being passed on.

Wright-Fisher model with recombination

Since the specific pairing of chromosomes only matters over a single generation, in the long term the haploid approximation is very good:

Each child in $i+1$ selects a parent uniformly at random from generation $i$.
With probability $r$ an additional parent is selected.
In this case, a breakpoint chosen uniformly on the chromosome, and everything to either the left or right replaced by the homologous section of the second parent's chromosome.
(Equivalent to selecting 2 parents for each child and letting the resulting sequences recombine with some probability.)

Model 1: Coalescent with Recombination

For fixed recombination rate $\rho=r/g$ in the limit $r\ll 1$, $g\ll 1$ and $N\gg 1$, the genealogical process is the coalescent with recombination (Hudson, 1983):

Coalescence rate: $T_c(k)=\binom{k}{2}\frac{1}{N}$
Recombination rate: $T_r(k)=\rho k$.
Recombination break points chosen uniformly along sequence: everything to the left descends from one parent, everything else to the other.
Each site possess a local tree.
Local trees may find MRCAs (grey sites) before grand (G)MRCA of the process.

CwR example ARG

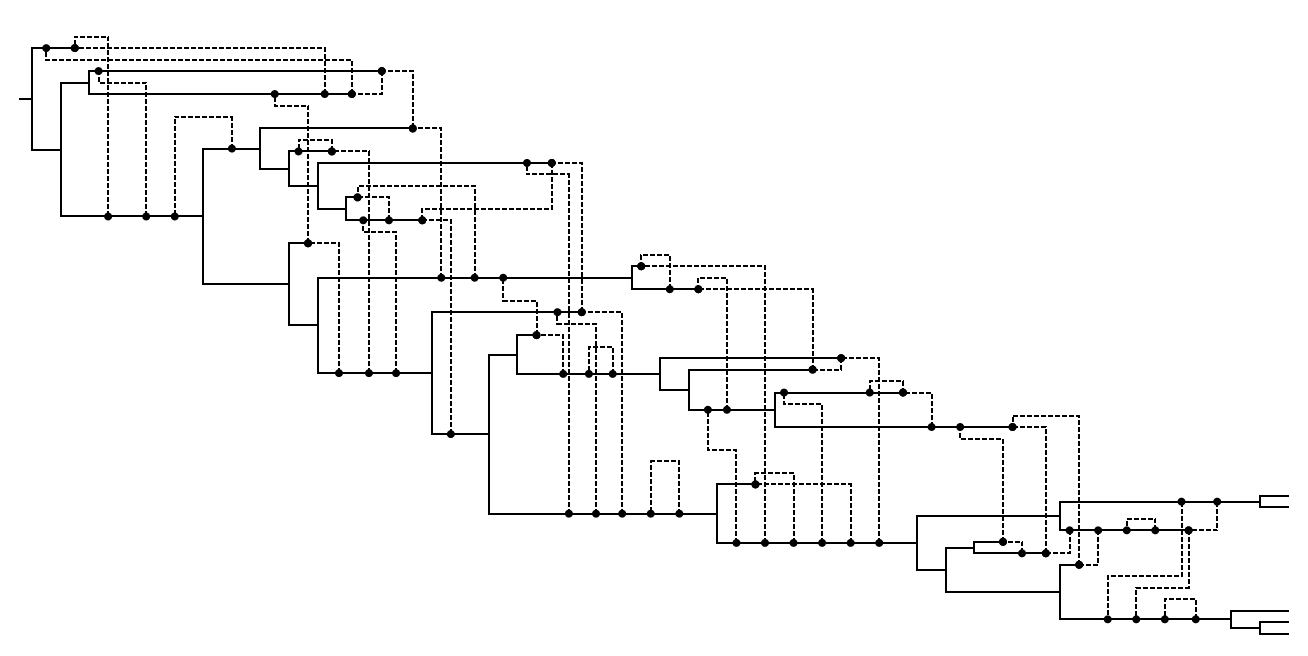
Coalescent with gene conversion

A gene conversion event refers to the replacement of a single contiguous stretch of sequence with a homologous stretch from a different parent. Incorporated into a modified CwR process by Wiuf and Hein (2000).

Allows similar patterns of site ancestry but with fewer events.
Model applicable to prokaryotic recombination.
Coalescence and recombination rates as for CwR.
Conversions initiate at randomly chosen starting sites and extend for $d$ sites where $P(d)=(1-\delta^{-1})^{d-1}\delta^{-1}$ (geometric distribution).

Bayesian inference of ARGs

Can easily write down an expression for the posterior distribution for the ARG given an alignment:

$$P(G,\rho,N,\mu|A) = \frac{1}{P(A)}P(A|G,\mu)P(G|\rho,N)P(\rho,N,\mu)$$

$G$ is the recombination graph,
$\rho$ is the recombination rate.

In practice, this is non-trivial since:

the likelihood for $G$, $P(A|G,\mu)$, is invariant under many features of $G$,
the likelihood surface often contains many distinct peaks, and
the state space of ARGs is huge: much larger than for trees.

Despite this, many approximate algorithms exist.

Algorithms for Bayesian ARG inference

Bacteria

Bacteria play critical roles in the health of animals and plants.
Many bacteria possess interesting and experimentally accessible evolutionary dynamics.
Bacterial genomes are measurably evolving over relatively short study periods.

Drummond & Rambaut, TIEE (2003)

Rainey & Travisano, Nature (1998)

Cartoon bacterial model

Effect of events can be plasmid transfer, insertion or homologous recombination.
Rate of recombination varies and is subject to selection.
Focus on homologous recombination: only event which doesn't alter the length of the sequence.

Bacterial Recombination Rates

For many bacteria, the ratio between the recombination rate and the mutation rate is extremely high.

Vos and Didelot, The ISME Journal (2009)

The Coalescent with Gene Conversion

Wiuf, 1999; Wiuf and Hein, 2000

Parameters
$1/N(t)$	Coalescence rate
$\rho_s$	Recombination rate
$\delta$	Expected tract length

Problem

The space of possible ancestral recombination graphs is extremely large. Even two samples have infinitely many distinct ancestries!

Full ARG

Approximation 1: ClonalFrame

Didelot et al., 2007 (ClonalFrame); Didelot and Wilson, 2015 (ClonalFrameML)

Approximation 2: ClonalOrigin

Didelot et al., 2010 (ClonalOrigin); Ansari and Didelot, 2014 (ClonalOrigin')

Our Goal

To conduct Bayesian inference of the full ARG under the ClonalOrigin model, optionally under non-trivial population size dynamics.

Inference under the ClonalOrigin Model

Inference follows the standard Bayesian phylogenetic tradition:

\begin{equation*} f(G,N,\mu,\rho,\delta|A) \propto P_{F}(A|G,\mu)f_{CGC}(G|N,\rho,\delta)f_{\text{prior}}(N ,\mu,\rho,\delta) \end{equation*}

where

$A$ is the sequence alignment,
$\mu$ are the substitution model parameters, and
$G$ is the full sample genealogy including clonal frame
$T$ and $M$ conversions $\{C_i\}_{i\in[1\ldots M]}$.

The genealogy density under ClonalOrigin model can be expanded

\begin{equation*} f_{CGC}(G|\rho',\delta,N)=\left(\prod_{i=1}^M f(C_i|T,N,\delta)\right)P(M|T,\rho)f_C(T|N) \end{equation*}

Identifiability

Despite using a simplified model, an infinite number of ARGs still possess the same likelihood given a sequence alignment.

Very important for an MCMC algorithm to propose state changes which minimize effect on likelihood.

Software implementation

tgvaughan.github.io/bacter

BEAST 2 package that performs inference under the ClonalOrigin model.
Joint inference of the clonal frame, recombinant edges and parameters.
Can be combined with usual variety of substitution models, parametric population models and parameter priors.
GUI analysis configuration via BEAUti.

Validation: Inference from simulated data

True ARG:

Randomly-selected ARG from MCMC:

Summary networks

True ARG:

Summary ARG from MCMC:

Application to Escherichia coli

Applied method to E. coli O157/O26 sequences collected by Tessy George (^mEpiLab, Massey University, New Zealand).
Sequences for 53 rMLST genes (21.1 kb total) from each of 23 human and cattle-derived isolates.
Analyzed using fixed expected tract length parameter and informative prior on conversion rate parameter.

Application to Escherichia coli

Bayesian Skyline Plots in Bacter

Bacter implements a non-parametric demographic history model inspired by the standard Bayesian Skyline Plot (Drummond et al., 2005).
In principle can reconstruct non-trivial dynamics from very few genomes.
In practice, this is limited by the computational expense of the algorithm.

Piecewise constant/linear population model

Inference example

Bacter limitations

Computational complexity scales with the number of proposed conversions.
- This can be arbitrarily large, even for small sample sets.
- Cannot use the BEAGLE phylogenetic likelihood library to speed things up due to peculiarities of ARG likelihood computation.
MCMC algorithm used does not intelligently locate conversions.
- Looking at addressing this in the near future.
Network summary algorithm can produce peculiar results.
- More research needs to be done to find a better algorithm.

Summary

It is important to be aware of the role recombination plays in shaping the phylogeny of a set of samples.
Recombination networks are distinct from (nested within!) species networks.
Network inference is both statistically and computationally demanding.
Model-based methods for inferring recombination networks exist.
Within BEAST 2, the available method is Bacter, which focuses on bacterial recombination.
This method will be taught in the following tutorial!