

What is a Population?


What is Phylodynamics?
- What does a phylogenetic tree tell us about a population?
- Places the emphasis on the population itself instead of the subset of individuals involved in a particular phylogeny.
- Term introduced by Grenfell et al. (2004) in the context of epidemiology, but modern phylodynamic methods are much more generally applied.
Connecting the dots...
Bayesian phylodynamics
- Generative models connect the population dynamics model to the observed sequence alignment.
- Use Bayesian inference to work backwards:
Why use sequence data?
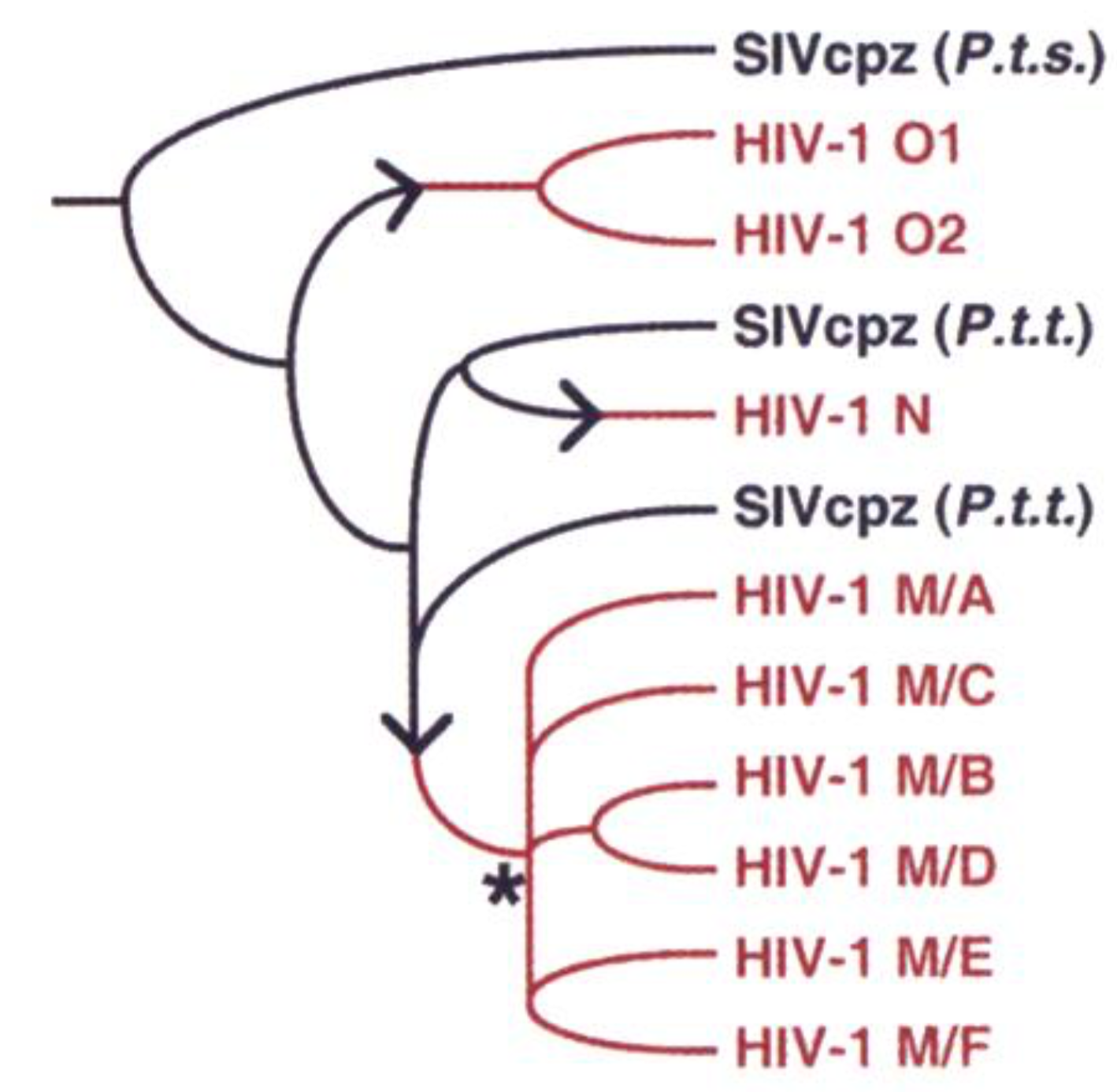
Sequence data can allow migration/transmission patterns (i.e. who infected whom) to be uncovered.
Why use sequence data?
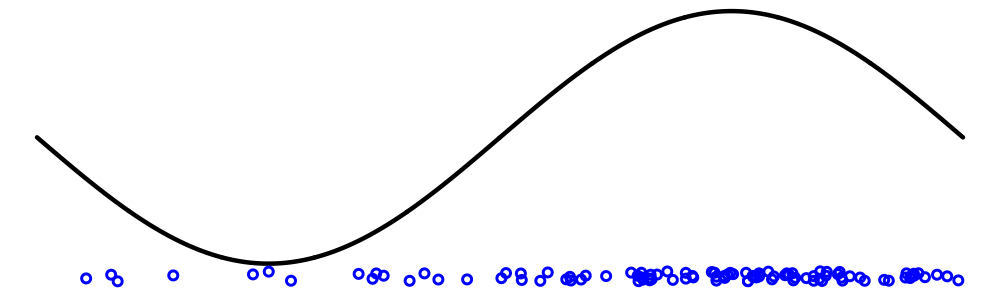
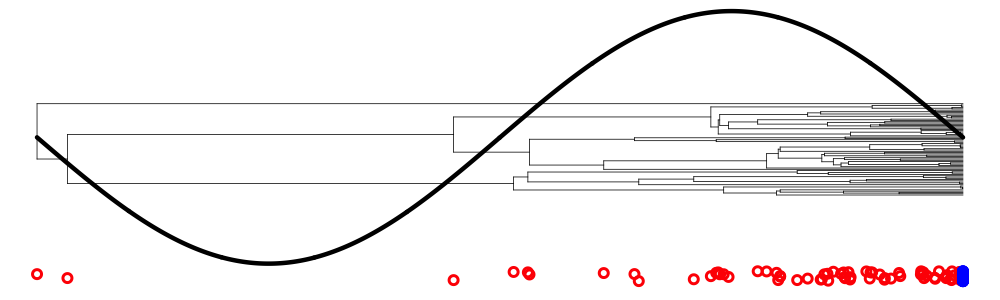
Genetic samples yield trees: information about events ancestral to samples.
Classes of phylodynamic models
- Coalescent models
- Originally developed by John Kingman in a series of papers in 1982.
- Extensions for dynamics and structured populations introduced by several authors.
- Birth-death models
- Theory for completely sampled contemporaneous trees developed by Elizabeth Thompson in her 1975 book "Human Evolutionary Trees".
- Theory for trees conditioned on number of samples and extensions to incomplete sampling, sampling through time, structured populations, etc. developed by Tanja Stadler from 2008.

Questions?
Birth-death models
Birth-death population dynamics
- Population size described by a positive integer.
- Changes through time according to a continuous time Markov process, similar to the substitution models we've already seen.
Can use a chemical reaction notation to describe rates and effects of possible events:
- Birth:
- $$X\overset{\lambda}{\longrightarrow} 2X$$
- Death:
- $$X\overset{\mu}{\longrightarrow} 0$$
The parameters $\lambda$ and $\mu$ are probabilities per [time unit] that any given individual experiences a birth or a death.
Example BD dynamics
Example BD dynamics
Birth-death branching process
Birth-death-sampling process
- The birth-death sampling process extends the birth-death process by incorporating a model for sample generation.
- This can be described using the following reactions:
- Birth: $X\overset{\lambda}{\longrightarrow}2X$
- Death: $X\overset{\mu}{\longrightarrow}0$
- Sampling (with removal): $X\overset{r\psi}{\longrightarrow}0$
- Sampling without removal: $X\overset{(1-r)\psi}{\longrightarrow}X$
Additionally, the model allows each surviving lineage at the end of the process (present day) to be sampled with probability $\rho$.
Birth-death-sampling trees
The sampled tree probability
The sampled tree probability
Gives rise to differential equations which can be solved to obtain the following tree probability: \begin{equation*} P(T|\lambda,\mu,\psi,r,t_0) = g(t_0) =\lambda^{n+m-1}\psi^{k+m}(4\rho)^n\prod_{i=0}^{n+m-1}\frac{1}{q(x_i)}\prod_{i=1}^{m}p_0(y_i)q(y_i) \end{equation*} where $q(t)=4\rho/g(t)$. [Stadler, J. Theor. Biol., 2010]
Birth-death parameterizations
There are several distinct parameterizations besides the basic $\lambda,\mu,\psi$ parameterization, including:
- Epidemiological parameterization:
-
- Effective reproductive number $R_e$ ($=\lambda/(\mu + r\psi$)
- Becoming uninfectious rate $\mu+r\psi$
- Sampling proportion $\psi/(\psi+\mu)$
- Macroevolutionary parameterization:
-
- Species diversification rate $\lambda - \mu$
- Turnover rate $\mu/\lambda$
- Fossilization rate $\psi$
Extension: time-dependence
- The birth-death skyline model allows piecewise-constant variation in rate parameters.

Example: Hepatitis C in Egypt
- Effective reproductive number $R_e(t)$ generalizes basic reproductive number $R_0=R_e(0)$.
- Analysis of 63 sequences, $R_e(t)=\lambda(t)/\mu(t)$.
Birth-death model assumptions
- Samples are members of a stochastically varying population that is on average exponentially growing with rate $\lambda-(\mu+r\psi)$.
- Sample fraction can be small, large or complete - tree prior is still valid.
- Sample number and times are assumed to be produced according to the model: deviation from this assumption results in biased inferences.
- Population is "well mixed", samples are drawn randomly.
Questions?
Coalescent phylodynamics
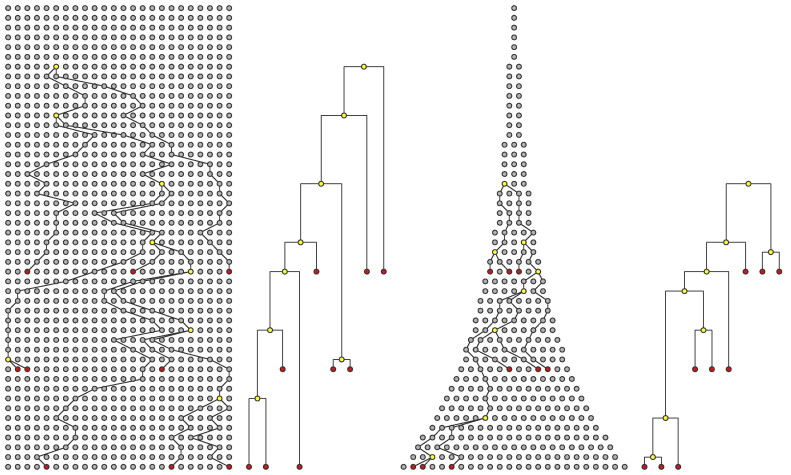
The Wright-Fisher Model
Wright-Fisher Model Assumptions
- Discrete generations.
- Individuals identical. (No structure.)
- Fixed offspring distribution (mean of 1)
- Constant + finite population size.
- An interpretation: population at equilibrium (carrying capacity).
Sampled WF phylogeny
Sampled WF phylogeny
- Generations between internal nodes related to population size.
- Can we quantify this relationship?
Sampled 2-individual phylogeny
Probability of coalescence in generation $i-m$: $P(m)=(1-p_{\textrm{coal}})^{m-1}p_{\textrm{coal}}$
Continuous time limit (large $N$, small $g$): $P(t)=e^{-\frac{1}{Ng}t}\frac{1}{Ng}$
The exponential distribution
Sampled k-individual phylogeny
Question: How can this be generalized to $k$ samples?
Answer: $p_{\text{coal}}=\frac{k(k-1)}{2}\frac{1}{N}=\binom{k}{2}\frac{1}{N}$
Kingman's coalescent
- Backward-time Markov process which produces sampled time trees.
- Equivalent to sampled trees produced by WF model when $N\gg k$ and $g\ll 1$.
- Times between coalescence events drawn from exponential distributions with rate $\binom{k}{2}\frac{1}{Ng}$.
- Interesting: expected time to MRCA is always $\leq \frac{2}{Ng}$, regardless of how many samples there are.
Effective population size
- If a real population were described precisely by a Wright-Fisher model with generation time $g$, the $N$ parameter in the coalescent would correspond to the real population size.
- However, real populations are more complicated:
- Random mating assumption is often violated,
- Offspring distribution may differ from that assumed by WF,
- Generations may be overlapping,
- ...
- We therefore define the effective population size $N_e$ to be the size of a statistically equivalent WF population. (We often also absorb other parameters such as $g$, the clock rate and ploidy into this number.)
Probability of a coalescent tree
Coalescent-based inference
- We can therefore infer demographic parameters like $N_e$ given a known phylogeny!
Extension: population size changes
 Kühnert et al., 2011
Kühnert et al., 2011
Non-parametric: Skyline plot
- Due to Pybus, Rambaut and Harvey, 2000.
- Directly yields ML estimates of population size in each interval.
Bayesian skyline
- Piecewise-constant population model: population size can only change at a fixed number of break points. Each time interval can contain several coalescent intervals.
- Uses MCMC to integrate over all possible break point positions in addition to $N_e$ within each time interval.
- Graphs of marginal probability of population size vs time appear smoothed due to averaging over possible histories.
Example: $N_e$ for HCV in Egypt
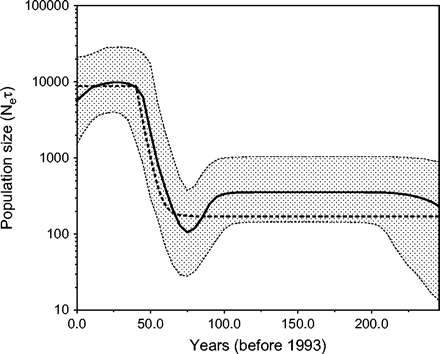
General assumptions of the coalescent
- Samples are members of a population that is at demographic equilibrium.
- Number of samples is small compared to the total population size.
- Necessary for WF-based derivation, not all derivations.
- Population is "well mixed", samples are drawn randomly.
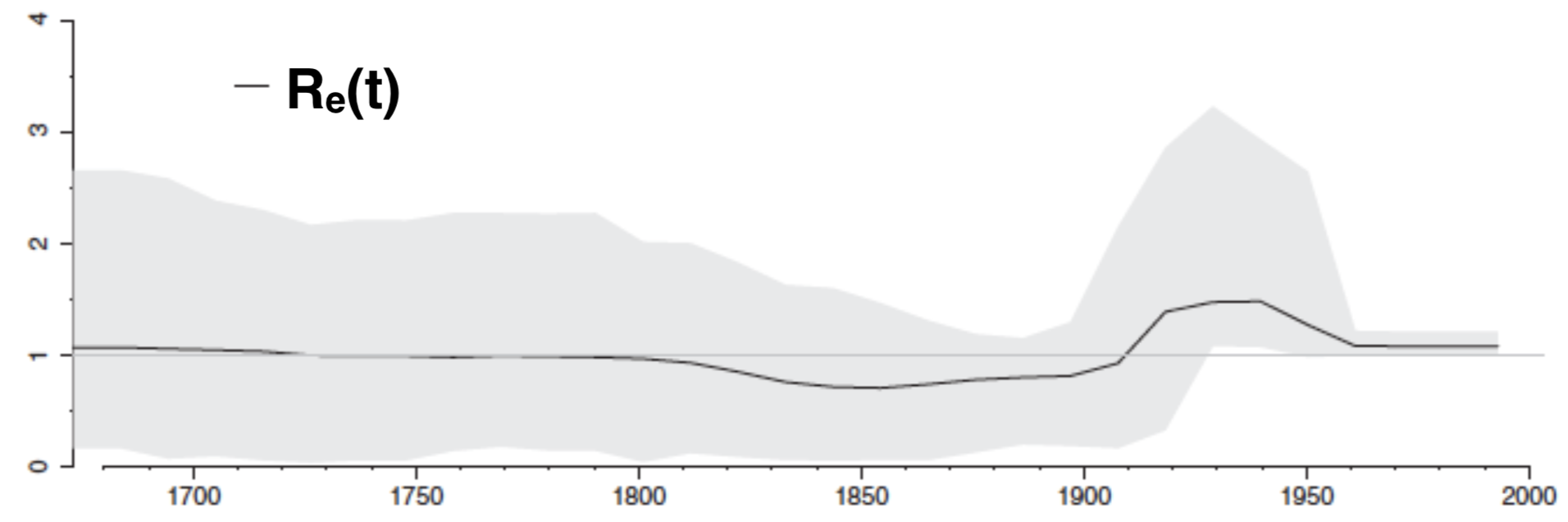
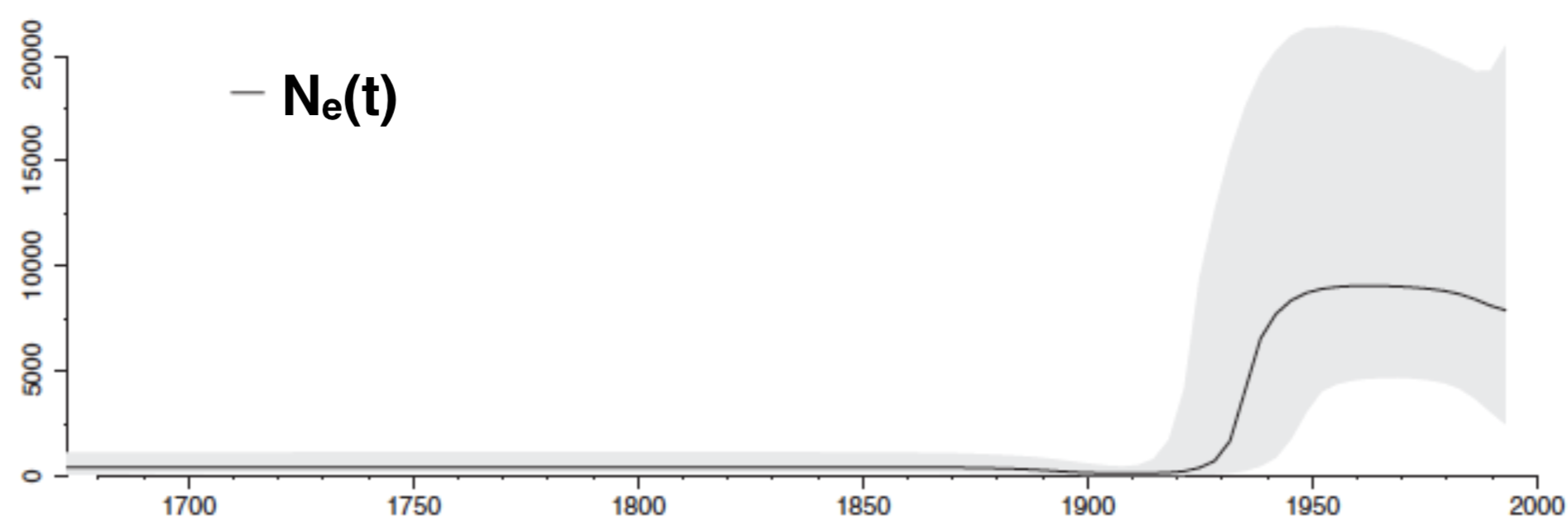
Birth-death vs coalescent HCV phylodynamics
Birth-death model can infer effective reproductive number dynamics:
Coalescent model can infer effective population size dynamics:
Conclusions
- Both birth-death and coalescent models probabilistically relate a population's demography to its phylogenetic history.
- Both allow for model-based inference of demographic and epidemiological parameters but may differ in their parameterization.
- Which model to use depends on what assumptions you are willing to make and what you want to infer.